注意力机制

注意力

在传统的机器学习模型中，尤其是在处理序列数据（如文本、语音、时间序列）时，模型通常需要将整个输入序列压缩成一个固定长度的向量（例如，使用RNN的最后一个隐藏状态），然后再基于这个向量进行后续操作（如翻译、分类）。对于短句，这还能工作，但对于长句，这个固定向量就会成为信息瓶颈，无法记住所有细节。

注意力机制(Attention Mechanism)的灵感来自人类的视觉处理系统，当你在阅读一本书的一页时，视线中的大部分内容实际上被忽视了，你更多的关注你正在阅读的那个词，这使你的大脑能够专注于最重要的事物，而忽视其他所有事物。

注意力一般分为两种：

(1) 自上而下的有意识的注意力，称为聚焦式注意力（Focus Attention）。聚焦式注意力是指有预定目的、依赖任务的，主动有意识地聚焦于某一对象的注意力。
(2) 自下而上的无意识的注意力，称为基于显著性的注意力（SaliencyBased Attention）。基于显著性的注意力是由外界刺激驱动的注意，不需要主动干预，也和任务无关。在目前的神经网络模型中，我们可以将最大汇聚（Max Pooling）、门控（Gating）机制近似地看作自下而上的基于显著性的注意力机制。

注意力机制的计算可以分为两步：一是在所有输入信息上计算注意力分布，二是根据注意力分布来计算输入信息的加权平均。

实例：我们用一个翻译示例来贯穿讲解注意力机制。

任务：将一句法语翻译成英语。
输入法语："Bonjour le monde"
目标英语："Hello world"

注意力分布

为了从 TT 个输入状态 k1,k2,⋯kT\mathbf k_1,\mathbf k_2,\cdots\mathbf k_T 中选择出和某个特定任务相关的信息，我们需要引入一个和输出相关的查询向量（QueryVector）。可以是动态生成的，也可以是可学习的参数。然后通过计算每个输入向量和查询向量之间的相关性，得到相应的权重系数。

αt=softmax(s(kt,q))\alpha_t=\text{softmax}(s(\mathbf k_t,\mathbf q))

其中 αt∈R\alpha_t\in\R 称为注意力分布（Attention Distribution），s(kt,q)s(\mathbf k_t,\mathbf q) 为注意力打分函数，可以使用以下几种方式来计算：

加性注意力：

s(kt,q)=vTtanh⁡(Wkkt+Wqq)s(\mathbf k_t,\mathbf q)=\mathbf v^T\tanh(\mathbf W_k\mathbf k_t+\mathbf W_q\mathbf q)

点积注意力：

s(kt,q)=kTqs(\mathbf k_t,\mathbf q)=\mathbf k^T\mathbf q

缩放点积注意力：

s(kt,q)=kTqDs(\mathbf k_t,\mathbf q)=\frac{\mathbf k^T\mathbf q}{\sqrt{D}}

当输入向量的维度 DD 比较高时，点积注意力的值通常有比较大的方差，从而导致Softmax函数的梯度会比较小。缩放点积注意力可以较好地解决这个问题。

双线性注意力：

s(kt,q)=kTWqs(\mathbf k_t,\mathbf q)=\mathbf k^T\mathbf W\mathbf q

双线性模型是一种泛化的点积模型。

注意力分布 αt\alpha_t 可以解释为在给定任务相关的查询 q\mathbf q 时，第 tt 个输入向量受关注的程度。

示例：开始计算上节实例中注意力分布，这是注意力的核心步骤。

首先，我们需要对句子进行编码。为了极度简化，我们假设每个单词已经由编码器（比如一个RNN）转换成了隐藏状态（Hidden States）。

输入序列 ["Bonjour", "le", "monde"] 对应的编码器隐藏状态（假设是2维向量，便于计算）:
h1 = [1.0, 0.5] (代表 "Bonjour")
h2 = [0.8, 1.2] (代表 "le")
h3 = [0.2, 1.5] (代表 "monde")

假设现在解码器要生成第一个英文单词 "Hello"。此时解码器的隐藏状态（初始状态）为 s0 = [0.8, 0.3]

我们需要计算当前解码器状态 s0 与每一个编码器状态 h_i 的相关度。我们用一个简单的点积来计算相关度得分。

s(h1, s0) = (0.8 * 1.0) + (0.3 * 0.5) = 0.8 + 0.15 = 0.95
s(h2, s0) = (0.8 * 0.8) + (0.3 * 1.2) = 0.64 + 0.36 = 1.00
s(h3, s0) = (0.8 * 0.2) + (0.3 * 1.5) = 0.16 + 0.45 = 0.61

得到原始分数：s = [0.95, 1.00, 0.61] 。我们使用 Softmax 函数转换为注意力分布。这是一个概率分布，即所有权重之和为1，这样才能体现关注度的分配。

得到注意力权重：α = [0.36, 0.38, 0.26]

现在，在生成英文单词 "Hello" 时，模型认为：

  • 38% 的注意力应该放在 "Bonjour" 上
  • 36% 的注意力放在 "le" 上
  • 26% 的注意力放在 "monde" 上

这看起来仍然有点奇怪，这是因为我们的初始权重是随机假设的。经过训练后，模型会学会调整参数，使得在生成"Hello"时，α1（对应"Bonjour"）的权重会接近1，而其他权重接近0。

注意力值

接下来一般采用软注意力（Soft Attention）对输入信息进行汇总，它是所有输入状态的加权和，权重就是上一步计算出的注意力权重。

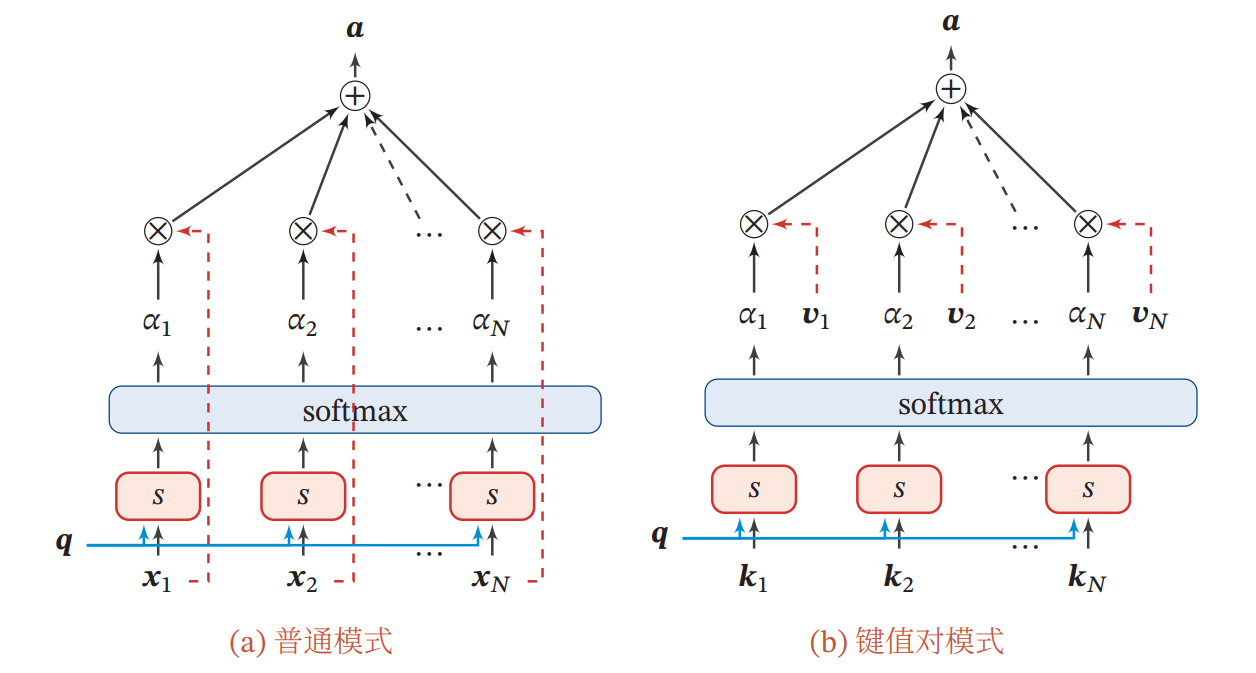
c=∑t=1Tαtkt\mathbf c=\sum_{t=1}^T\alpha_t\mathbf k_t

更一般地，我们可以用键值对（key-value pair）格式来表示输入信息，其中 key 用来计算注意力分布 αt\alpha_t， value 用来计算聚合信息。给定查询向量 q\mathbf q 时，注意力函数为

c=∑t=1Tαtvt=∑t=1Tsoftmax(s(kt,q))vt\mathbf c=\sum_{t=1}^T\alpha_t\mathbf v_t= \sum_{t=1}^T\text{softmax}(s(\mathbf k_t,\mathbf q))\mathbf v_t

示例：继续计算上下文向量（Context Vector）

C0 = α1 * h1 + α2 * h2 + α3 * h3 = [0.716, 1.026]

这个上下文向量不再是某个单一的输入单词的向量，它包含了所有输入单词的信息，但主要由当前解码步骤最需要关注的单词（根据权重）所主导。

现在我们可以将上下文向量传递给解码器。解码器将 s0 和 C0 连接起来，或者通过另一个神经网络，来计算最终预测 "Hello" 的概率。

我们可以可视化注意力权重，清楚地看到模型在生成某个输出词时关注了哪些输入词，这大大增加了模型的透明度。

注意力机制不仅是机器翻译的关键，更是Transformer架构的基石，催生了BERT、GPT等革命性模型。它已经成为现代深度学习最重要的概念之一。

多头注意力

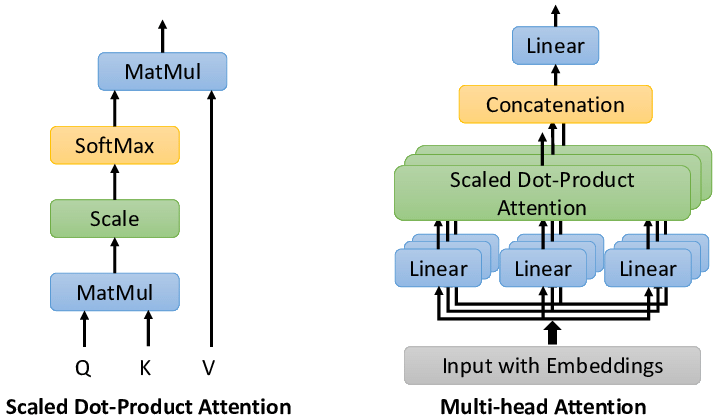
多头注意力（Multi-Head Attention）是利用多个查询 Q=[q1,q1,⋯ ,qM]\mathbf Q=[\mathbf q_1,\mathbf q_1,\cdots,\mathbf q_M]，来并行地从输入信息中选取多组信息。每个注意力有自己的线性变换矩阵，关注输入信息的不同部分。

自注意力机制

自注意力(Self-Attention)是注意力机制的一种特殊形式，它允许输入序列中的每个元素都与序列中的所有其他元素建立联系。

为了提高模型能力，自注意力模型经常采用 Query-Key-Value，模式，其计算过程如下图所示，其中红色字母表示矩阵的维度。

自注意力机制每个位置都能直接访问序列中所有位置的信息。不依赖序列顺序，适合处理各种结构化数据。

假设输入序列 X=[x1,x2,⋯xN]\mathbf X=[\mathbf x_1,\mathbf x_2,\cdots\mathbf x_N]，输出蓄序列 H=[h1,h2,⋯hN]\mathbf H=[\mathbf h_1,\mathbf h_2,\cdots\mathbf h_N]

(1) 对于每个输入 xi\mathbf x_i，我们首先将其线性映射到三个不同的空间，得到查询
向量 qi\mathbf q_i、键向量 xi\mathbf x_i 和值向量 xi\mathbf x_i。对于整个输入序列 X\mathbf X，线性映射过程可以简写为

Q=WqXK=WkXV=WvX\mathbf Q=\mathbf W_q\mathbf X \\ \mathbf K=\mathbf W_k\mathbf X \\ \mathbf V=\mathbf W_v\mathbf X

(2) 由于自注意力模型中通常使用点积来计算注意力打分，输出向量序列可以简写为

H=Vsoftmax(KTQDk)\mathbf H=\mathbf V\text{softmax}\left(\frac{\mathbf K^T\mathbf Q}{\sqrt{D_k}}\right)

其中 softmax 为按列进行归一化的函数。