异常检测
远离其它内围点(inlier)的数据通常被定义为离群值(outlier),也称异常值。异常检测(anomaly detection)分为离群点检测以及新奇值检测两种。
- Outlier Detection(OD):离群值检测。训练数据包含异常值,这些异常值被定义为远离其他样本。
- Novelty Detection(ND):新奇值检测。训练数据没有异常值,我们检测新样本是否为异常值。在这种情况下,异常值也被称为新奇值。
在异常检测领域,LOF 算法和 Isolation Forest 算法已经被指出是性能最优、识别效果最好的算法。
椭圆包络
椭圆包络(Elliptic Envelope)算法假设数据为正态分布,并基于这个假设对数据进行稳健的协方差估计(Robust covariance),从而为中心数据点拟合出一个忽视了离群点的椭圆。从而使用 Mahalanobis 距离进行异常检测。 该策略如下图所示
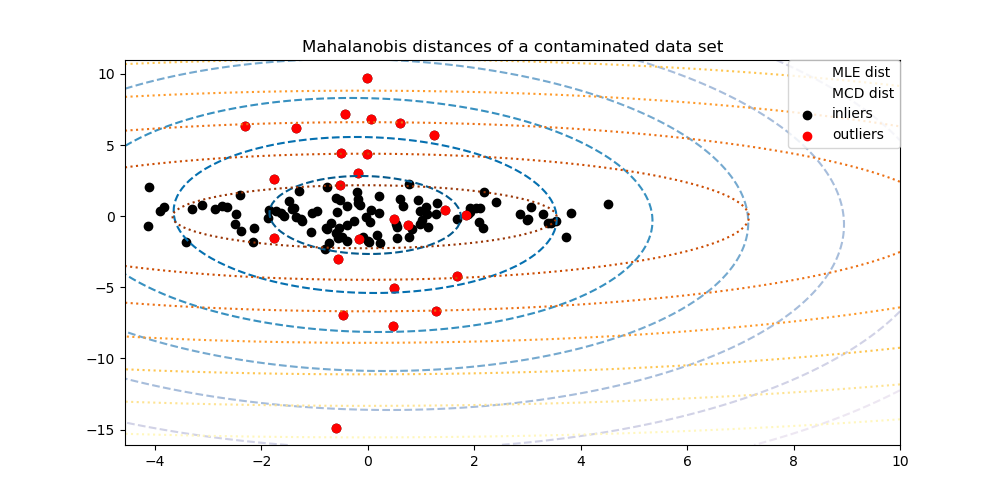
One-Class SVM
One-Class SVM也是属于支持向量机大家族的,但是它和传统的基于监督学习的支持向量机不同,它是无监督学习的方法,也就是说,它不需要我们标记训练集的输出标签。
One-Class SVM的思路非常简单,在特征空间中训练一个超球面,将训练数据全部包起来,在球外的样本就认为是异常点。期望最小化这个超球体,从而最小化异常点数据的影响。

现介绍一种拟合超球体的思想 SVDD (support vector domain description)。假设产生的超球体中心数据点为 ,超球体半径 ,超球体表面积 被最小化。要求所有训练数据点 到中心的距离小于 ,同时构造一个惩罚系数为 的松弛变量 ,松弛变量的作用就是允许少数异常点在超球面之外。优化问题如下
然后,采用Lagrange乘子法求解
其中 ,令 对参数的偏导为零,可得到
带入Lagrangian函数
其中 。上面的向量内积也可以像SVM那样引入核函数
通常使用高斯核(并无明确的理论支持),之后像SVM一样求解。计算数据点到圆心的距离,从而判断是否为异常值。
孤立森林
Isolation Forest 简称 iForest,译作孤立森林或隔离森林,由南京大学周志华等人共同开发。孤立森林是一种适用于连续数据的无监督异常检测方法。在孤立森林中,异常被定义为容易被孤立的离群点(more likely to be separated),可以将其理解为分布稀疏且离密度高的群体较远的点。 在特征空间里,分布稀疏的区域表示事件发生在该区域的概率很低,因而可以认为落在这些区域里的数据是异常的。
给定样本矩阵
包含 个样本, 个特征。其中,第 个样本的特征向量为 。
iForest:该算法得益于随机森林的思想,与随机森林由大量决策树组成一样,iForest 也由大量的二叉树组成,称为 iTree(isolation tree)。iTree 树和随机森林的决策树不太一样,是一个完全随机的过程。
在做 iTree 分裂决策时,由于我们没有目标变量,所以没法根据信息增益或基尼指数来生成树。iTree 使用的是随机选择划分特征,然后在这个特征的范围内再随机选择划分阈值,对树进行二叉分裂。直到树的深度达到限定阈值或者样本数只剩一个。
从统计意义上来说,这种随机分割的策略下,那些密度很高的簇是需要被切很多次才能被孤立,但是那些密度很低的点很容易就可以被孤立。由于异常值的数量较少且与大部分样本的疏离性,因此,异常值会被更早的孤立出来,也即异常值会距离 iTree 的根节点更近,而正常值则会距离根节点有更远的距离。
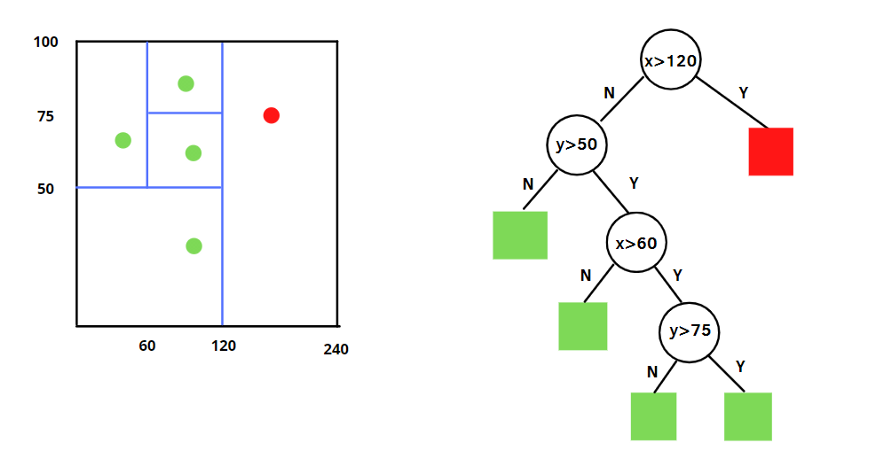
一颗 iTree 的结果往往不可信,iForest 算法通过构建多颗二叉树,整合所有树的结果,判断异常值。
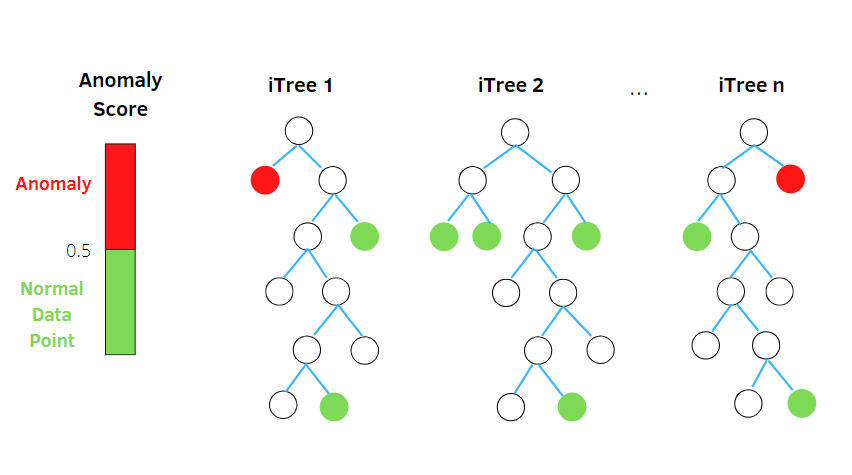
超参数:iForest 算法主要有两个参数:一个是二叉树的个数;另一个是训练单棵iTree时候抽取样本的数目。
通常树的数量越多,算法越稳定,但不是越多越好。经验表明,当树的个数 后,平均路径长度都已经收敛了,故推荐 。 如果特征和样本规模比较大,可以适当增加。
然后,采样决策树的训练样本时,普通的随机森林要采样的样本个数等于训练集个数。但是iForest不需要采样这么多,一般来说,采样个数要远远小于训练集个数。原因是我们的目的是异常点检测,只需要部分的样本我们一般就可以将异常点区别出来了。
实验表明,当设定树的个数 ,每棵树的样本数 的时候,iForest 在大多数情况下就可以取得不错的效果。这也体现了算法的简单,高效。
另外,还要给每棵树设置最大深度 ,它近似等于树的平均深度。之所以对树的深度做限制,是因为我们只关心路径长度较短的点,它们更可能是异常点,而并不关心那些路径很长的正常点。


路径长度:数据点 在树中的路径长度定义为
其中,为样本 从树的根节点到叶子节点经过的边的数量,即分裂次数。 表示和样本 同在一个叶子结点样本的个数。 是一个修正值,使得异常和正常样本的路径长度差异更大。
其中 为欧拉常数。可以简单的理解,如果样本快速落入叶子结点,并且该叶子结点的样本数较少,那么其为异常样本的可能性较大。
异常得分:(Anomaly Score)这里把路径长度的值映射到之间
其中, 为抽样子集的样本数。 为样本在所有树的路径长度均值, 估计路径的平均长度。
的取值越接近于1,则是异常点的概率也越大。异常情况的判断分以下几种
- 当 时, ,则是异常点的可能性越高;
- 当 时, ,则是正常点的可能性越高;
- 当大部分的训练样本的 时, ,说明整个数据集都没有明显的异常值。
一般我们可以设置 的一个阈值,大于阈值的才认为是异常点。
优点:iForest目前是异常点检测最常用的算法之一,它的优点非常突出,它具有线性时间复杂度。因为每棵树随机采样独立生成,所以孤立森林具有很好的处理大数据的能力和速度,可以进行并行化处理,因此可部署在大规模分布式系统上来加速运算。不同于 KMeans、DBSCAN 等算法,iForest不需要计算有关距离、密度等指标,可大幅度提升速度,减小系统开销
缺点:但是iForest也有一些缺点,比如不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度和该维度的随机一个特征,建完树后仍然有大量的维度没有被使用,导致算法可靠性降低。此时推荐降维后使用,或者考虑使用One-Class SVM。
下图是一个 iForest 示例:
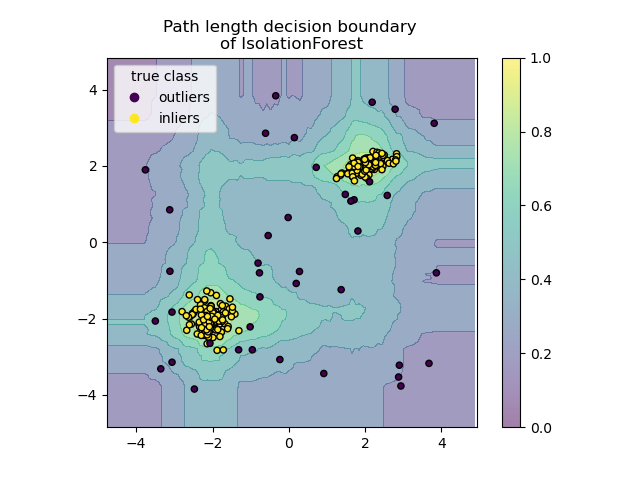
局部离群因子
局部离群因子算法:(Local Outlier Factor,LOF)是一种典型的基于密度的高精度离群点检测方法。它不需要对数据的分布做太多要求,还能量化每个数据点的异常程度(outlierness)。它测量给定数据点相对于相邻数据点的局部密度偏差,称为局部离群因子。
先定义数据点 到 可达距离(reachability distance)
其中, 为数据点 和 之间的距离。 是点 第 个最近邻的距离。
然后,定义局部可达密度(local reachability density):点 到 个最近邻的平均可达距离的倒数
其中, 是点 的 个最近邻的集合,即和点 距离小于 的近邻集合,易知 邻域数据点的个数 。

最后,定义局部离群因子(local outlier factor)为其 个最近邻的平均局部密度与其本身密度的比值。
正常数据点与其近邻有着相似的局部密度,此时 ;而异常数据点则比近邻的局部密度要小得多 。LOF 算法的优点是考虑到数据集的局部和全局属性。异常值不是按绝对值确定的,而是相对于它们的邻域点密度确定的。当数据集中存在不同密度的不同集群时,LOF 表现良好,比较适用于中等高维的数据集。
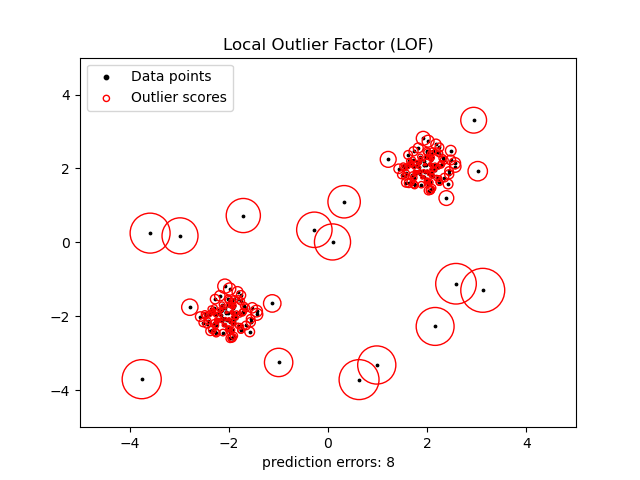
近邻数 通常的选择策略
- 大于一个局部簇必须包含的最小数量,小于局部簇最大数量。
- 在实践中,通常取 ,可以使算法有很好的表现。
- 当离群点的比例较高时(大于 10% 时), 应该取更大的值。








