k近邻算法

K近邻法(k-nearest neighbor, k-NN)是一种基本分类与回归方法，其工作机制十分简单粗暴：给定某个测试样本，kNN基于某种距离度量在训练集中找出与其距离最近的k个带有真实标记的训练样本，然后给基于这k个邻居的真实标记来进行预测：通常分类任务采用投票法，回归任务则采用平均法。接下来本篇主要就kNN分类进行讨论。

k值的选择

KNN

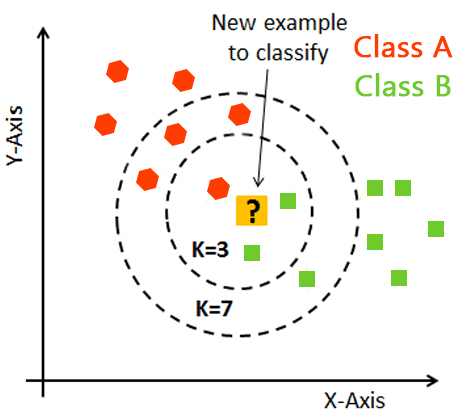
上图给出了k近邻分类器的一个示意图。可以发现：kNN虽然是一种监督学习方法，但是它却没有显式的训练过程，而是当有新样本需要预测时，才来计算出最近的k个邻居，因此kNN是一种典型的懒惰学习方法，

很容易看出：kNN算法的核心在于k值的选取以及距离的度量。k值选取太小，模型很容易受到噪声数据的干扰，例如：极端地取k=1，若待分类样本正好与一个噪声数据距离最近，就导致了分类错误；若k值太大， 则在更大的邻域内进行投票，此时模型的预测能力大大减弱，例如：极端取k=训练样本数，就相当于模型根本没有学习，所有测试样本的预测结果都是一样的。一般地我们都通过交叉验证法来选取一个适当的k值。

当 k=1k=1 时，也称为最近邻分类器(Nearest Neighbor Classifier)。最近邻分类器的一个性质是，当样本量 N→∞N\to\infty 时，其分类错误率不超过贝叶斯分类器错误率的两倍。

K-D Tree

KNN应用的一个实践问题是如何快速搜索 k 近邻点。KD树是一种对高维空间中的实例点进行存储以便对其进行快速检索的树状数据结构。KD树是二叉树，表示对高维空间的一个划分。构造 KD 树相当于不断地用垂直于坐标轴的超平面将高维空间切分，构成一系列的高维超矩形区域。

通常，依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的中位数为切分点，这样得到的KD树是平衡的。注意，平衡的KD树搜索时的效率未必是最优的。

Ball Tree

为了解决KD树在更高维度上的低效率问题，开发了球树数据结构。球树递归地将数据划分为由重心定义的节点CC和半径rr，使得节点中的每个点都位于由CC和rr定义的超球体内。通过使用三角形不等式 ∣x+y∣≤∣x∣+∣y∣|x+y|\leq|x|+|y|，近邻搜索的候选点数量会减少。